Esoteric Other Worlds

Exploring Mysticism, and Parapsychology.This blog is also an attempt to promote awareness of a Modern Universal Paradigm known as Multi-Dimensional Science. It offers a "Scientific" testable Hypothesis for a more "objective" understanding of claimed Psychic and Spiritual Phenomena. A link to this subject should be found onsite or alternatively easily traceable via a word search. Please note that the Internet articles here may not reflect the views of the Blogger.

Monday 4 March 2013

The Fourth Dimension

The concept of the Fourth Dimension has been used as an explanation for the manifestation of claimed psyhic, and mystical phenomena. Unfortunately, like Quantum Mechanics its understanding is incomplete without the development of Multi-Dimensional Science..

http://www.p2pfoundation.net/Multi-Dimensional_Science

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (February 2009)

3D projection of a tesseract undergoing a simple rotation in four dimensional space.

In mathematics, four-dimensional space ("4D") is an abstract concept derived by generalizing the rules of three-dimensional space. It has been studied by mathematicians and philosophers for almost three hundred years, both for its own interest and for the insights it offered into mathematics and related fields.
Algebraically it is generated by applying the rules of vectors and coordinate geometry to a space with four dimensions. In particular a vector with four elements (a 4-tuple) can be used to represent a position in four-dimensional space. The space is a Euclidean space, so has a metric and norm, and so all directions are treated as the same: the additional dimension is indistinguishable from the other three.
In modern physics, space and time are unified in a four-dimensional Minkowski continuum called spacetime, whose metric treats the time dimension differently from the three spatial dimensions (see below for the definition of the Minkowski metric/pairing). Spacetime is thus not a Euclidean space.

[edit] History

[edit] Vectors

Mathematically four-dimensional space is simply a space with four spatial dimensions, that is a space that needs four parameters to specify a point in it. For example a general point might have position vector a, equal to

$\mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \end{pmatrix}.$

This can be written in terms of the four standard basis vectors (e₁, e₂, e₃, e₄), given by

$\mathbf{e}_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}; \mathbf{e}_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}; \mathbf{e}_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}; \mathbf{e}_4 = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix},$

so the general vector a is

$\mathbf{a} = a_1\mathbf{e}_1 + a_2\mathbf{e}_2 + a_3\mathbf{e}_3 + a_4\mathbf{e}_4.$

Vectors add, subtract and scale as in three dimensions.
The dot product of Euclidean three-dimensional space generalizes to four dimensions as

$\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 + a_4 b_4.$

It can be used to calculate the norm or length of a vector,

$\left| \mathbf{a} \right| = \sqrt{\mathbf{a} \cdot \mathbf{a} } = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2 + {a_4}^2},$

and calculate or define the angle between two vectors as

$\theta = \arccos{\frac{\mathbf{a} \cdot \mathbf{b}}{\left|\mathbf{a}\right| \left|\mathbf{b}\right|}}.$

Minkowski spacetime is four-dimensional space with geometry defined by a nondegenerate pairing different from the dot product:

$\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 - a_4 b_4.$

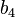As an example, the distance squared between the points (0,0,0,0) and (1,1,1,0) is 3 in both the Euclidean and Minkowskian 4-spaces, while the distance squared between (0,0,0,0) and (1,1,1,1) is 4 in Euclidean space and 2 in Minkowski space; increasing $b_4$ actually decreases the metric distance. This leads to many of the well known apparent "paradoxes" of relativity.
The cross product is not defined in four dimensions. Instead the exterior product is used for some applications, and is defined as follows:

$\begin{align} \mathbf{a} \wedge \mathbf{b} = (a_1b_2 - a_2b_1)\mathbf{e}_{12} + (a_1b_3 - a_3b_1)\mathbf{e}_{13} + (a_1b_4 - a_4b_1)\mathbf{e}_{14} + (a_2b_3 - a_3b_2)\mathbf{e}_{23} \\ + (a_2b_4 - a_4b_2)\mathbf{e}_{24} + (a_3b_4 - a_4b_3)\mathbf{e}_{34}. \end{align}$

This is bivector valued, with bivectors in four dimensions forming a six-dimensional linear space with basis (e₁₂, e₁₃, e₁₄, e₂₃, e₂₄, e₃₄). They can be used to generate rotations in four dimensions.

[edit] Orthogonality and vocabulary

In the familiar 3-dimensional space that we live in there are three coordinate axes — usually labeled x, y, and z — with each axis orthogonal (i.e. perpendicular) to the other two. The six cardinal directions in this space can be called up, down, east, west, north, and south. Positions along these axes can be called altitude, longitude, and latitude. Lengths measured along these axes can be called height, width, and depth.
Comparatively, 4-dimensional space has an extra coordinate axis, orthogonal to the other three, which is usually labeled w. To describe the two additional cardinal directions, Charles Howard Hinton coined the terms ana and kata, from the Greek words meaning "up toward" and "down from", respectively. A length measured along the w axis can be called spissitude, as coined by Henry More.

[edit] Geometry

The geometry of 4-dimensional space is much more complex than that of 3-dimensional space, due to the extra degree of freedom.
Just as in 3 dimensions there are polyhedra made of two dimensional polygons, in 4 dimensions there are polychora (4-polytopes) made of polyhedra. In 3 dimensions there are 5 regular polyhedra known as the Platonic solids. In 4 dimensions there are 6 convex regular polychora, the analogues of the Platonic solids. Relaxing the conditions for regularity generates a further 58 convex uniform polychora, analogous to the 13 semi-regular Archimedean solids in three dimensions.

Regular polytopes in four dimensions
(Displayed as orthogonal projections in each Coxeter plane of symmetry)
A₄	BC₄		F₄	H₄
5-cell	tesseract	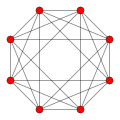16-cell	24-cell	120-cell	600-cell

In 3 dimensions, a circle may be extruded to form a cylinder. In 4 dimensions, there are several different cylinder-like objects. A sphere may be extruded to obtain a spherical cylinder (a cylinder with spherical "caps"), and a cylinder may be extruded to obtain a cylindrical prism. The Cartesian product of two circles may be taken to obtain a duocylinder. All three can "roll" in 4-dimensional space, each with its own properties.
In 3 dimensions, curves can form knots but surfaces cannot (unless they are self-intersecting). In 4 dimensions, however, knots made using curves can be trivially untied by displacing them in the fourth direction, but 2-dimensional surfaces can form non-trivial, non-self-intersecting knots in 4-dimensional space ^[9]. Because these surfaces are 2-dimensional, they can form much more complex knots than strings in 3-dimensional space can. The Klein bottle is an example of such a knotted surface^{[citation needed]}. Another such surface is the real projective plane^{[citation needed]}.

[edit] Hypersphere

Stereographic projection of a Clifford torus: the set of points (cos(a), sin(a), cos(b), sin(b)), which is a subset of the 3-sphere.

The set of points in Euclidean 4-space having the same distance R from a fixed point P₀ forms a hypersurface known as a 3-sphere. The hyper-volume of the enclosed space is:

$\mathbf V = \begin{matrix} \frac{1}{2} \end{matrix} \pi^2 R^4$

This is part of the Friedmann–Lemaître–Robertson–Walker metric in General relativity where R is substituted by function R(t) with t meaning the cosmological age of the universe. Growing or shrinking R with time means expanding or collapsing universe, depending on the mass density inside.^[10]

[edit] Cognition

Research using virtual reality finds that humans in spite of living in a three-dimensional world can without special practice make spatial judgments based on the length of, and angle between, line segments embedded in four-dimensional space.^[11] The researchers noted that "the participants in our study had minimal practice in these tasks, and it remains an open question whether it is possible to obtain more sustainable, definitive, and richer 4D representations with increased perceptual experience in 4D virtual environments."^[11] In another study,^[12] the ability of humans to orient themselves in 2D, 3D and 4D mazes has been tested. Each maze consisted of four path segments of random length and connected with orthogonal random bends, but without branches or loops (i.e. actually labyrinths). The graphical interface was based on John McIntosh's free 4D Maze game.^[13] The participating persons had to navigate through the path and finally estimate the linear direction back to the starting point. The researchers found that some of the participants were able to mentally integrate their path after some practice in 4D (the lower dimensional cases were for comparison and for the participants to learn the method).

[edit] Dimensional analogy

A net of a tesseract

To understand the nature of four-dimensional space, a device called dimensional analogy is commonly employed. Dimensional analogy is the study of how (n − 1) dimensions relate to n dimensions, and then inferring how n dimensions would relate to (n + 1) dimensions.^[14]
Dimensional analogy was used by Edwin Abbott Abbott in the book Flatland, which narrates a story about a square that lives in a two-dimensional world, like the surface of a piece of paper. From the perspective of this square, a three-dimensional being has seemingly god-like powers, such as ability to remove objects from a safe without breaking it open (by moving them across the third dimension), to see everything that from the two-dimensional perspective is enclosed behind walls, and to remain completely invisible by standing a few inches away in the third dimension.
By applying dimensional analogy, one can infer that a four-dimensional being would be capable of similar feats from our three-dimensional perspective. Rudy Rucker illustrates this in his novel Spaceland, in which the protagonist encounters four-dimensional beings who demonstrate such powers.

[edit] Cross-sections

As a three-dimensional object passes through a two-dimensional plane, a two-dimensional being would only see a cross-section of the three-dimensional object. For example, if a balloon passed through a sheet of paper, a being on the paper would see a circle gradually grow larger, then smaller again. Similarly, if a four-dimensional object passed through three-dimensions, we would see a three-dimensional cross-section of the four-dimensional object–for example, a sphere.^[15]

[edit] Projections

A useful application of dimensional analogy in visualizing the fourth dimension is in projection. A projection is a way for representing an n-dimensional object in n − 1 dimensions. For instance, computer screens are two-dimensional, and all the photographs of three-dimensional people, places and things are represented in two dimensions by projecting the objects onto a flat surface. When this is done, depth is removed and replaced with indirect information. The retina of the eye is also a two-dimensional array of receptors but the brain is able to perceive the nature of three-dimensional objects by inference from indirect information (such as shading, foreshortening, binocular vision, etc.). Artists often use perspective to give an illusion of three-dimensional depth to two-dimensional pictures.
Similarly, objects in the fourth dimension can be mathematically projected to the familiar 3 dimensions, where they can be more conveniently examined. In this case, the 'retina' of the four-dimensional eye is a three-dimensional array of receptors. A hypothetical being with such an eye would perceive the nature of four-dimensional objects by inferring four-dimensional depth from indirect information in the three-dimensional images in its retina.
The perspective projection of three-dimensional objects into the retina of the eye introduces artifacts such as foreshortening, which the brain interprets as depth in the third dimension. In the same way, perspective projection from four dimensions produces similar foreshortening effects. By applying dimensional analogy, one may infer four-dimensional "depth" from these effects.
As an illustration of this principle, the following sequence of images compares various views of the 3-dimensional cube with analogous projections of the 4-dimensional tesseract into three-dimensional space.

Cube	Tesseract	Description
		The image on the left is a cube viewed face-on. The analogous viewpoint of the tesseract in 4 dimensions is the cell-first perspective projection, shown on the right. One may draw an analogy between the two: just as the cube projects to a square, the tesseract projects to a cube.Note that the other 5 faces of the cube are not seen here. They are obscured by the visible face. Similarly, the other 7 cells of the tesseract are not seen here because they are obscured by the visible cell.
		The image on the left shows the same cube viewed edge-on. The analogous viewpoint of a tesseract is the face-first perspective projection, shown on the right. Just as the edge-first projection of the cube consists of two trapezoids, the face-first projection of the tesseract consists of two frustums.The nearest edge of the cube in this viewpoint is the one lying between the red and green faces. Likewise, the nearest face of the tesseract is the one lying between the red and green cells.
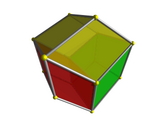		On the left is the cube viewed corner-first. This is analogous to the edge-first perspective projection of the tesseract, shown on the right. Just as the cube's vertex-first projection consists of 3 deltoids surrounding a vertex, the tesseract's edge-first projection consists of 3 hexahedral volumes surrounding an edge. Just as the nearest vertex of the cube is the one where the three faces meet, so the nearest edge of the tesseract is the one in the center of the projection volume, where the three cells meet.
		A different analogy may be drawn between the edge-first projection of the tesseract and the edge-first projection of the cube. The cube's edge-first projection has two trapezoids surrounding an edge, while the tesseract has three hexahedral volumes surrounding an edge.
		On the left is the cube viewed corner-first. The vertex-first perspective projection of the tesseract is shown on the right. The cube's vertex-first projection has three tetragons surrounding a vertex, but the tesseract's vertex-first projection has four hexahedral volumes surrounding a vertex. Just as the nearest corner of the cube is the one lying at the center of the image, so the nearest vertex of the tesseract lies not on boundary of the projected volume, but at its center inside, where all four cells meet.Note that only three faces of the cube's 6 faces can be seen here, because the other 3 lie behind these three faces, on the opposite side of the cube. Similarly, only 4 of the tesseract's 8 cells can be seen here; the remaining 4 lie behind these 4 in the fourth direction, on the far side of the tesseract.

[edit] Shadows

A concept closely related to projection is the casting of shadows.

If a light is shone on a three dimensional object, a two-dimensional shadow is cast. By dimensional analogy, light shone on a two-dimensional object in a two-dimensional world would cast a one-dimensional shadow, and light on a one-dimensional object in a one-dimensional world would cast a zero-dimensional shadow, that is, a point of non-light. Going the other way, one may infer that light shone on a four-dimensional object in a four-dimensional world would cast a three-dimensional shadow.
If the wireframe of a cube is lit from above, the resulting shadow is a square within a square with the corresponding corners connected. Similarly, if the wireframe of a tesseract were lit from “above” (in the fourth direction), its shadow would be that of a three-dimensional cube within another three-dimensional cube. (Note that, technically, the visual representation shown here is actually a two-dimensional shadow of the three-dimensional shadow of the four-dimensional wireframe figure.)

[edit] Bounding volumes

Dimensional analogy also helps in inferring basic properties of objects in higher dimensions. For example, two-dimensional objects are bounded by one-dimensional boundaries: a square is bounded by four edges. Three-dimensional objects are bounded by two-dimensional surfaces: a cube is bounded by 6 square faces. By applying dimensional analogy, one may infer that a four-dimensional cube, known as a tesseract, is bounded by three-dimensional volumes. And indeed, this is the case: mathematics shows that the tesseract is bounded by 8 cubes. Knowing this is key to understanding how to interpret a three-dimensional projection of the tesseract. The boundaries of the tesseract project to volumes in the image, not merely two-dimensional surfaces.

[edit] Visual scope

Being three-dimensional, we are only able to see the world with our eyes in two dimensions. A four-dimensional being would be able to see the world in three dimensions. For example, it would be able to see all six sides of an opaque box simultaneously, and in fact, what is inside the box at the same time, just as we can see the interior of a square on a piece of paper. It would be able to see all points in 3-dimensional space simultaneously, including the inner structure of solid objects and things obscured from our three-dimensional viewpoint. Our brains receive images in the second dimension and use reasoning to help us "picture" three-dimensional objects. Just as a four-dimensional creature would probably receive multiple three-dimensional pictures.^{[citation needed]}

[edit] Limitations

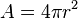Reasoning by analogy from familiar lower dimensions can be an excellent intuitive guide, but care must be exercised not to accept results that are not more rigorously tested. For example, consider the formulas for the circumference of a circle $C = 2\pi r$ and the surface area of a sphere: $A = 4\pi r^2$ . One might be tempted to suppose that the surface volume of a hypersphere is 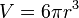$V=6\pi r^3$ , or perhaps 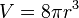$V=8\pi r^3$ , but either of these would be wrong. The correct formula is $V = 2\pi^2 r^3$ .^[8]

[edit] See also

Wikisource has original text related to this article:

Flatland

Euclidean space
Euclidean geometry
4-manifold
Exotic R⁴
Dimension
Four-dimensionalism
Fifth dimension
Sixth dimension
Polychoron
Polytope
List of geometry topics
Block Theory of the Universe
Flatland, a book by Edwin A. Abbott about two- and three-dimensional spaces, to understand the concept of four dimensions
Sphereland, an unofficial sequel to Flatland
Charles Howard Hinton
Dimensions, a set of films about two-, three- and four-dimensional polytopes
List of four-dimensional games

[edit] References

^ Coxeter, H. S. M. (1973). Regular Polytopes, Dover Publications, Inc., p. 141.
^ Coxeter, H. S. M. (1973). Regular Polytopes, Dover Publications, Inc., pp. 142–143.
^ Rudolf v.B. Rucker, editor Speculations on the Fourth Dimension: Selected Writings of Charles H. Hinton, p. vii, Dover Publications Inc., 1980 ISBN 0-486-23916-0
^ Hinton, Charles Howard (1904). Fourth Dimension. ISBN 1-5645-9708. http://www.archive.org/details/fourthdimension00hintarch.
^ Gardner, Martin (1975). Mathematical Carnival. Knopf Publishing. pp. 42, 52–53. ISBN 0 14 02.2041 0.
^ Hermann Minkowski, "Raum und Zeit", 80. Versammlung Deutscher Naturforscher (Köln, 1908). Published in Physikalische Zeitschrift 10 104–111 (1909) and Jahresbericht der Deutschen Mathematiker-Vereinigung 18 75–88 (1909). For an English translation, see Lorentz et al. (1952).
^ C Møller (1952). The Theory of Relativity. Oxford UK: Clarendon Press. p. 93. ISBN 0-19-851256-2.
^ ^a ^b Coxeter, H. S. M. (1973). Regular Polytopes, Dover Publications, Inc., p. 119.
^ J. Scott Carter, Masahico Saito Knotted Surfaces and Their Diagrams
^ Ray d'Inverno (1992), Introducing Einstein's Relativity, Clarendon Press, chp. 22.8 Geometry of 3-spaces of constant curvature, p.319ff, ISBN 0-19-859653-7
^ ^a ^b Ambinder MS, Wang RF, Crowell JA, Francis GK, Brinkmann P. (2009). Human four-dimensional spatial intuition in virtual reality. Psychon Bull Rev. 16(5):818-23. doi:10.3758/PBR.16.5.818 PMID 19815783 online supplementary material
^ Aflalo TN, Graziano MS (2008). Four-Dimensional Spatial Reasoning in Humans. Journal of Experimental Psychology: Human Perception and Performance 34(5):1066-1077. doi:10.1037/0096-1523.34.5.1066 Preprint
^ John McIntosh's four dimensional maze game. Free software
^ Michio Kaku (1994). Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the Tenth Dimension, Part I, chapter 3, The Man Who "Saw" the Fourth Dimension (about tesseracts in years 1870–1910). ISBN 0-19-286189-1.
^ Gamow, George (1988). One Two Three . . . Infinity: Facts and Speculations of Science (3rd ed.). Courier Dover Publications. p. 68. ISBN 0-486-25664-2. http://books.google.com/books?id=EZbcwk6SkhcC., Extract of page 68

[edit] External links

Wikibooks has a book on the topic of: Special Relativity

v t e Dimension

Dimensional spaces	One Two Three Four Five Six Seven Eight n-dimensions Spacetime Projective space Hyperplane

Polytopes and Shapes	Simplex Hypercube Hyperrectangle Demihypercube Cross-polytope n-sphere

Concepts and mathematics	Cartesian coordinates Linear algebra Geometric algebra Conformal geometry Reflection Rotation Plane of rotation Space Fractal dimension Multiverse

Category

Retrieved from "http://en.wikipedia.org/w/index.php?title=Four-dimensional_space&oldid=540728807"

Categories:

Blogger Reference Link http://www.p2pfoundation.net/Multi-Dimensional_Science