From Wikipedia, the free encyclopedia
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit (the basic unit of quantum information) can be transmitted exactly (in principle) from one location to another, without the qubit being transmitted through the intervening space. It is useful for quantum information processing. However, it does not immediately transmit classical information, and therefore cannot be used for communication at superluminal (faster than light) speed. Quantum teleportation is unrelated to the common term teleportation – it does not transport the system itself, and does not concern rearranging particles to copy the form of an object.
The seminal paper first expounding the idea was published by C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres and W. K. Wootters in 1993.[1] In November 2012, the first quantum teleportation from one macroscopic object to another was reported.[2][3]
Presently, the record distance for quantum teleportation is 143 km (89 mi).[4]
1. An EPR pair is generated, one qubit sent to location A, the other to B.
2. At location A, a Bell measurement of the EPR pair qubit and the qubit to be teleported (for example, quantum state of a photon) is performed, yielding two classical bits of information. Both qubits are destroyed.
of a photon) is performed, yielding two classical bits of information. Both qubits are destroyed.
3. Using the classical channel, the two bits are sent from A to B. (This is the only potentially time-consuming step, due to speed-of-light considerations.)
4. At location B, the EPR pair qubit is modified (if necessary), using the two bits to select the correct one of four possible quantum states. A qubit identical to that chosen for teleportation (for example, quantum state of a photon) results.
of a photon) results.
 . (A qubit may be represented as a superposition of states, labeled
. (A qubit may be represented as a superposition of states, labeled  and
and  .) Assume that this quantum state is not known to Alice and she would like to send this state to Bob. Ostensibly, Alice has the following options:
.) Assume that this quantum state is not known to Alice and she would like to send this state to Bob. Ostensibly, Alice has the following options:
Option 2 is forbidden by the no-broadcast theorem.
Option 3 (classical teleportation) has also been formally shown to be impossible. (See the no-teleportation theorem.) This is another way to say that quantum information cannot be measured reliably.
Thus, Alice seems to face an impossible problem. A solution was discovered by Bennett, et al. The components of a maximally entangled two-qubit state are distributed to Alice and Bob. The protocol then involves Alice and Bob interacting locally with the qubit(s) in their possession and Alice sending two classical bits to Bob. In the end, the qubit in Bob's possession will be in the desired state.
Alice applies a unitary operation on the qubits ac and measures the result to obtain two classical bits. In this process, the two qubits are destroyed. Bob's qubit, b, now contains information about c; however, the information is somewhat randomized. More specifically, Bob's qubit b is in one of four states uniformly chosen at random and Bob cannot obtain any information about c from his qubit.
Alice provides her two measured classical bits, which indicate which of the four states Bob possesses. Bob applies a unitary transformation which depends on the classical bits he obtains from Alice, transforming his qubit into an identical re-creation of the qubit c.
 Suppose Alice has a qubit that she wants to teleport to Bob. This qubit can be written generally, in bra-ket notation, as:
Suppose Alice has a qubit that she wants to teleport to Bob. This qubit can be written generally, in bra-ket notation, as: 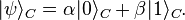
Our quantum teleportation scheme requires Alice and Bob to share a maximally entangled state beforehand, for instance one of the four Bell states

So, Alice has two particles (C, the one she wants to teleport, and A, one of the entangled pair), and Bob has one particle, B. In the total system, the state of these three particles is given by
The crucial step, the local measurement done by Alice on the Bell basis, is done. It is clear how to proceed further. Alice now has complete knowledge of the state of the three particles; the result of her Bell measurement tells her which of the four states the system is in. She simply has to send her results to Bob through a classical channel. Two classical bits can communicate which of the four results she obtained.
After Bob receives the message from Alice, he will know which of the four states his particle is in. Using this information, he performs a unitary operation on his particle to transform it to the desired state :
:
Experimentally, the projective measurement done by Alice may be achieved via a series of laser pulses directed at the two particles.
 is the Controlled NOT gate.
is the Controlled NOT gate.
If Alice has a particle which is entangled with a particle owned by Bob, and Bob teleports it to Carol, then afterwards, Alice's particle is entangled with Carol's.
A more symmetric way to describe the situation is the following: Alice has one particle, Bob two, and Carol one. Alice's particle and Bob's first particle are entangled, and so are Bob's second and Carol's particle:
 dimensional state space. To teleport, Alice makes a partial measurement on the two particles in her possession in some entangled basis on the
dimensional state space. To teleport, Alice makes a partial measurement on the two particles in her possession in some entangled basis on the 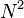 dimensional subsystem. This measurement has
dimensional subsystem. This measurement has 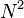 equally probable outcomes, which are then communicated to Bob classically. Bob recovers the desired state by sending his particle through an appropriate unitary gate.
equally probable outcomes, which are then communicated to Bob classically. Bob recovers the desired state by sending his particle through an appropriate unitary gate.
 denotes the composition of maps. This describes the channel in the Schrödinger picture.
denotes the composition of maps. This describes the channel in the Schrödinger picture.
Taking adjoint maps in the Heisenberg picture, the success condition becomes
 is
is 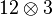 while that of
while that of  is
is  .
.
 is
is 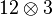 while that of
while that of  is
is  . Bob then applies a corresponding local operation Ψi on system 3. On the combined system, this is described by
. Bob then applies a corresponding local operation Ψi on system 3. On the combined system, this is described by
 .
.
Therefore the channel Φ is defined by
The seminal paper first expounding the idea was published by C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres and W. K. Wootters in 1993.[1] In November 2012, the first quantum teleportation from one macroscopic object to another was reported.[2][3]
Presently, the record distance for quantum teleportation is 143 km (89 mi).[4]
Contents |
[edit] Protocol
The prerequisites for quantum teleportation are a qubit that is to be teleported, a conventional communication channel capable of transmitting two classical bits (i.e., one of four states), and means of generating an entangled EPR pair of qubits, performing a Bell measurement on the EPR pair, and manipulating the quantum state of one of the pair. The protocol is then as follows:1. An EPR pair is generated, one qubit sent to location A, the other to B.
2. At location A, a Bell measurement of the EPR pair qubit and the qubit to be teleported (for example, quantum state
 of a photon) is performed, yielding two classical bits of information. Both qubits are destroyed.
of a photon) is performed, yielding two classical bits of information. Both qubits are destroyed.3. Using the classical channel, the two bits are sent from A to B. (This is the only potentially time-consuming step, due to speed-of-light considerations.)
4. At location B, the EPR pair qubit is modified (if necessary), using the two bits to select the correct one of four possible quantum states. A qubit identical to that chosen for teleportation (for example, quantum state
 of a photon) results.
of a photon) results.[edit] Experimental results
Work in 1998 verified the initial results,[5] and in August 2004 increased the distance of teleportation to 600 meters using optical fiber.[6] The longest distance yet claimed to be achieved for quantum teleportation is 143 km (89 mi) in May 2012 between the two Canary Islands of La Palma and Tenerife off the Atlantic coast of north Africa.[7] This is a milestone to potential applications, since it corresponds to the minimum distance between the ground and orbiting satellites. In April 2011, experimenters reported that they had demonstrated teleportation of wave packets of light up to a bandwidth of 10 MHz while preserving strongly nonclassical superposition states.[8][9][edit] Motivation
Suppose Alice has a qubit in some arbitrary quantum state . (A qubit may be represented as a superposition of states, labeled
. (A qubit may be represented as a superposition of states, labeled  and
and  .) Assume that this quantum state is not known to Alice and she would like to send this state to Bob. Ostensibly, Alice has the following options:
.) Assume that this quantum state is not known to Alice and she would like to send this state to Bob. Ostensibly, Alice has the following options:- She can attempt to physically transport the qubit to Bob.
- She can broadcast this (quantum) information, and Bob can obtain the information via some suitable receiver.
- She can perhaps measure the unknown qubit in her possession. The results of this measurement would be communicated to Bob, who then prepares a qubit in his possession accordingly, to obtain the desired state. (This hypothetical process is called classical teleportation.)
Option 2 is forbidden by the no-broadcast theorem.
Option 3 (classical teleportation) has also been formally shown to be impossible. (See the no-teleportation theorem.) This is another way to say that quantum information cannot be measured reliably.
Thus, Alice seems to face an impossible problem. A solution was discovered by Bennett, et al. The components of a maximally entangled two-qubit state are distributed to Alice and Bob. The protocol then involves Alice and Bob interacting locally with the qubit(s) in their possession and Alice sending two classical bits to Bob. In the end, the qubit in Bob's possession will be in the desired state.
[edit] A summary
Assume that Alice and Bob share an entangled qubit ab. That is, Alice has one half, a, and Bob has the other half, b. Let c denote the qubit Alice wishes to transmit to Bob.Alice applies a unitary operation on the qubits ac and measures the result to obtain two classical bits. In this process, the two qubits are destroyed. Bob's qubit, b, now contains information about c; however, the information is somewhat randomized. More specifically, Bob's qubit b is in one of four states uniformly chosen at random and Bob cannot obtain any information about c from his qubit.
Alice provides her two measured classical bits, which indicate which of the four states Bob possesses. Bob applies a unitary transformation which depends on the classical bits he obtains from Alice, transforming his qubit into an identical re-creation of the qubit c.
[edit] The result

Quantum circuit representation of quantum teleportation
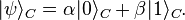
Our quantum teleportation scheme requires Alice and Bob to share a maximally entangled state beforehand, for instance one of the four Bell states
 ,
, ,
, ,
, .
.

So, Alice has two particles (C, the one she wants to teleport, and A, one of the entangled pair), and Bob has one particle, B. In the total system, the state of these three particles is given by
The crucial step, the local measurement done by Alice on the Bell basis, is done. It is clear how to proceed further. Alice now has complete knowledge of the state of the three particles; the result of her Bell measurement tells her which of the four states the system is in. She simply has to send her results to Bob through a classical channel. Two classical bits can communicate which of the four results she obtained.
After Bob receives the message from Alice, he will know which of the four states his particle is in. Using this information, he performs a unitary operation on his particle to transform it to the desired state
 :
:- If Alice indicates her result is
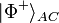 , Bob knows his qubit is already in the desired state and does nothing. This amounts to the trivial unitary operation, the identity operator.
, Bob knows his qubit is already in the desired state and does nothing. This amounts to the trivial unitary operation, the identity operator.
- If the message indicates
 , Bob would send his qubit through the unitary gate given by the Pauli matrix
, Bob would send his qubit through the unitary gate given by the Pauli matrix
- If Alice's message corresponds to
 , Bob applies the gate
, Bob applies the gate
- Finally, for the remaining case, the appropriate gate is given by
Experimentally, the projective measurement done by Alice may be achieved via a series of laser pulses directed at the two particles.
[edit] Remarks
- After this operation, Bob's qubit will take on the state
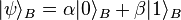 , and Alice's qubit becomes (undefined) part of an entangled state. Teleportation does not result in the copying of qubits, and hence is consistent with the no cloning theorem.
, and Alice's qubit becomes (undefined) part of an entangled state. Teleportation does not result in the copying of qubits, and hence is consistent with the no cloning theorem. - There is no transfer of matter or energy involved. Alice's particle has not been physically moved to Bob; only its state has been transferred. The term "teleportation", coined by Bennett, Brassard, Crépeau, Jozsa, Peres and Wootters, reflects the indistinguishability of quantum mechanical particles.
- For every qubit teleported, Alice needs to send Bob two classical bits of information. These two classical bits do not carry complete information about the qubit being teleported. If an eavesdropper intercepts the two bits, she may know exactly what Bob needs to do in order to recover the desired state. However, this information is useless if she cannot interact with the entangled particle in Bob's possession.
[edit] Alternative description
In the literature, one might find alternative, but completely equivalent, descriptions of the teleportation protocol given above. Namely, the unitary transformation that is the change of basis (from the standard product basis into the Bell basis) can also be implemented by quantum gates. Direct calculation shows that this gate is given by is the Controlled NOT gate.
is the Controlled NOT gate.[edit] Entanglement swapping
Teleportation can be applied not just to pure states, but also mixed states, that can be regarded as the state of a single subsystem of an entangled pair. The so-called entanglement swapping is a simple and illustrative example.If Alice has a particle which is entangled with a particle owned by Bob, and Bob teleports it to Carol, then afterwards, Alice's particle is entangled with Carol's.
A more symmetric way to describe the situation is the following: Alice has one particle, Bob two, and Carol one. Alice's particle and Bob's first particle are entangled, and so are Bob's second and Carol's particle:
___
/ \
Alice-:-:-:-:-:-Bob1 -:- Bob2-:-:-:-:-:-Carol
\___/
Now, if Bob performs a projective measurement on his two particles in the Bell state basis and communicates the results to Carol, as per the teleportation scheme described above, the state of Bob's first particle can be teleported to Carol's. Although Alice and Carol never interacted with each other, their particles are now entangled.[edit] N-state particles
One can imagine how the teleportation scheme given above might be extended to N-state particles, i.e. particles whose states lie in the N dimensional Hilbert space. The combined system of the three particles now has an dimensional state space. To teleport, Alice makes a partial measurement on the two particles in her possession in some entangled basis on the
dimensional state space. To teleport, Alice makes a partial measurement on the two particles in her possession in some entangled basis on the 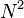 dimensional subsystem. This measurement has
dimensional subsystem. This measurement has 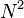 equally probable outcomes, which are then communicated to Bob classically. Bob recovers the desired state by sending his particle through an appropriate unitary gate.
equally probable outcomes, which are then communicated to Bob classically. Bob recovers the desired state by sending his particle through an appropriate unitary gate.[edit] General teleportation scheme
[edit] General description
A general teleportation scheme can be described as follows. Three quantum systems are involved. System 1 is the (unknown) state ρ to be teleported by Alice. Systems 2 and 3 are in a maximally entangled state ω that are distributed to Alice and Bob, respectively. The total system is then in the state denotes the composition of maps. This describes the channel in the Schrödinger picture.
denotes the composition of maps. This describes the channel in the Schrödinger picture.Taking adjoint maps in the Heisenberg picture, the success condition becomes
 is
is 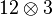 while that of
while that of  is
is  .
.[edit] Further details
The proposed channel Φ can be described more explicitly. To begin teleportation, Alice performs a local measurement on the two subsystems (1 and 2) in her possession. Assume the local measurement have effects is
is 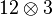 while that of
while that of  is
is  . Bob then applies a corresponding local operation Ψi on system 3. On the combined system, this is described by
. Bob then applies a corresponding local operation Ψi on system 3. On the combined system, this is described by .
.Therefore the channel Φ is defined by
[edit] See also
[edit] References
| This article includes a list of references, but its sources remain unclear because it has insufficient inline citations. (June 2012) |
- Specific
- ^ C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. K. Wootters, Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels, Phys. Rev. Lett. 70, 1895-1899 (1993) (online).
- ^ The Physics arXiv Blog (November 15, 2012). "First Teleportation from One Macroscopic Object to Another". MIT Technology Review. http://www.technologyreview.com/view/507531/first-teleportation-from-one-macroscopic-object-to-another/. Retrieved November 17, 2012.
- ^ Bao, Xiao-Hui; Xu, Xiao-Fan; Li, Che-Ming; Yuan, Zhen-Sheng; Lu, Chao-Yang; Pan, Jian-wei (November 13, 2012). "Quantum teleportation between remote atomic-ensemble quantum memories". arXiv. http://arxiv.org/abs/1211.2892. Retrieved November 17, 2012.
- ^ Ma, X. S.; Herbst, T.; Scheidl, T.; Wang, D.; Kropatschek, S.; Naylor, W.; Wittmann, B.; Mech, A. et al. (2012). "Quantum teleportation over 143 kilometres using active feed-forward". Nature 489 (7415): 269–273. doi:10.1038/nature11472. PMID 22951967.
- ^ D. Boschi; S. Branca1, F. De Martini1, L. Hardy, and S. Popescu (1998). "Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels". Physical Review Letters 80 (6): 1121. arXiv:quant-ph/9710013. Bibcode 1998PhRvL..80.1121B. doi:10.1103/PhysRevLett.80.1121.
- ^ Rupert Ursin (August 2004). "Quantum teleportation across the Danube". Nature. http://www.nature.com/nature/journal/v430/n7002/full/430849a.html. Retrieved 2010-05-22.
- ^ Xiao-song Ma, Thomas Herbst, Thomas Scheidl, Daqing Wang, Sebastian Kropatschek, William Naylor, Alexandra Mech, Bernhard Wittmann, Johannes Kofler, Elena Anisimova, Vadim Makarov, Thomas Jennewein, Rupert Ursin, Anton Zeilinger (17 May 2012). "Quantum teleportation using active feed-forward between two Canary Islands". http://arxiv.org/abs/1205.3909. Retrieved 2012-05-24.
- ^ Lee, Noriyuki; Hugo Benichi, Yuishi Takeno, Shuntaro Takeda, James Webb, Elanor Huntington, and Akira Furusawa (April 2011). "Teleportation of Nonclassical Wave Packets of Light". Science 332 (6027): 330–333. arXiv:1205.6253. Bibcode 2011Sci...332..330L. doi:10.1126/science.1201034. http://www.sciencemag.org/content/332/6027/330.abstract. Retrieved 2011-04-26.
- ^ Trute, Peter. "Quantum teleporter breakthrough". The University Of New South Wales. http://www.unsw.edu.au/news/pad/articles/2011/apr/Quantum_teleport_paper.html. Retrieved 17 April 2011.
- General
- Theoretical proposal:
- C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. K. Wootters, Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels, Phys. Rev. Lett. 70, 1895-1899 (1993) (pdf). This is the seminal paper that laid out the entanglement protocol.
- L. Vaidman, Teleportation of Quantum States, Phys. Rev. A 49, 1473-1476 (1994)
- G Brassard, S Braunstein, R Cleve, Teleportation as a Quantum Computation, Physica D 120 43-47 (1998)
- A. Peres, "What is actually teleported?", IBM Journal of Research and Development, Vol. 48, Issue 1, (2004)(this document online)
- G. Rigolin, Quantum Teleportation of an Arbitrary Two Qubit State and its Relation to Multipartite Entanglement, Phys. Rev. A 71 032303 (2005)(this document online)
- Shi-Biao Zheng, "Scheme for approximate conditional teleportation of an unknown atomic state without the Bell-state measurement", Phys. Rev. A 69, 064302 (2004).
- W. B. Cardoso, A. T. Avelar, B. Baseia, and N. G. de Almeida, "Teleportation of entangled states without Bell-state measurement", Phys. Rev. A 72, 045802 (2005).
- Michael N. Leuenberger, Michael E. Flatte, David D. Awschalom, "Teleportation of Electronic Many-Qubit States Encoded in the Electron Spin of Quantum Dots via Single Photons", Phys. Rev. Lett. 94, 107401 (2005).
- First experiments with photons:
- D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, A. Zeilinger, Experimental Quantum Teleportation, Nature 390, 6660, 575-579 (1997).
- D. Boschi, S. Branca, F. De Martini, L. Hardy, & S. Popescu, Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 80, 6, 1121-1125 (1998)
- Y.-H. Kim, S.P. Kulik, and Y. Shih, Quantum teleportation of a polarization state with a complete bell state measurement, Phys. Rev. Lett. 86, 1370 (2001).
- I. Marcikic, H. de Riedmatten, W. Tittel, H. Zbinden, N. Gisin, Long-Distance Teleportation of Qubits at Telecommunication Wavelengths, Nature, 421, 509 (2003)
- R. Ursin et al., Quantum Teleportation Link across the Danube, Nature 430, 849 (2004)
- First experiments with atoms:
- M. Riebe, H. Häffner, C. F. Roos, W. Hänsel, M. Ruth, J. Benhelm, G. P. T. Lancaster, T. W. Körber, C. Becher, F. Schmidt-Kaler, D. F. V. James, R. Blatt, Deterministic Quantum Teleportation with Atoms, Nature 429, 734-737 (2004)
- M. D. Barrett, J. Chiaverini, T. Schaetz, J. Britton, W. M. Itano, J. D. Jost, E. Knill, C. Langer, D. Leibfried, R. Ozeri, D. J. Wineland, Deterministic Quantum Teleportation of Atomic Qubits, Nature 429, 737 (2004).
- S. Olmschenk, D. N. Matsukevich, P. Maunz, D. Hayes, L.-M. Duan, and C. Monroe, Quantum Teleportation between Distant Matter Qubits, Science 323, 486 (2009).
[edit] External links
- signandsight.com:"Spooky action and beyond" - Interview with Prof. Dr. Anton Zeilinger about quantum teleportation. Date: 2006-02-16
- Quantum Teleportation at IBM
- Physicists Succeed In Transferring Information Between Matter And Light
- Quantum telecloning: Captain Kirk's clone and the eavesdropper
- Teleportation-based approaches to universal quantum computation
- Teleportation as a quantum computation
- Quantum teleportation with atoms: quantum process tomography
- Entangled State Teleportation
- Fidelity of quantum teleportation through noisy channels by
- TelePOVM— A generalized quantum teleportation scheme
- Entanglement Teleportation via Werner States
- Quantum Teleportation of a Polarization State
- The Time Travel Handbook: A Manual of Practical Teleportation & Time Travel
- letters to nature: Deterministic quantum teleportation with atoms
- Quantum teleportation with a complete Bell state measurement
- Welcome to the quantum Internet. Science News, Aug. 16 2008.
- Quantum experiments - interactive.
- “A (mostly serious) introduction to quantum teleportation for non-physicists”
| |||||||||||||||||||||||||||||||||||||||





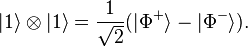





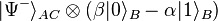
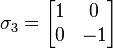



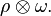





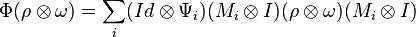






No comments:
Post a Comment