Monday, 4 March 2013

Quantum Mechanics

 
Certain interpretations of Quantum Mechanics/Theory has helped to give parapsychology some degree of scientific credibility. However, such an approach is totally incomplete without the evolving project of Multi-Dimensional Science.
 
 
RS
 
 
 
 
From Wikipedia, the free encyclopedia


Jump to: navigation, search

For a generally accessible and less technical introduction to the topic, see Introduction to quantum mechanics.
Quantum mechanics
Qm template pic 4.svg
Introduction
Glossary · History
Quantum mechanics (QM – also known as quantum physics, or quantum theory) is a branch of physics dealing with physical phenomena at microscopic scales, where the action is on the order of the Planck constant. Quantum mechanics departs from classical mechanics primarily at the quantum realm of atomic and subatomic length scales. Quantum mechanics provides a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter.
In advanced topics of quantum mechanics, some of these behaviors are macroscopic and only emerge at extreme (i.e., very low or very high) energies or temperatures.[citation needed] The name quantum mechanics derives from the observation that some physical quantities can change only in discrete amounts (Latin quanta), and not in a continuous (cf. analog) way. For example, the angular momentum of an electron bound to an atom or molecule is quantized.[1] In the context of quantum mechanics, the wave–particle duality of energy and matter and the uncertainty principle provide a unified view of the behavior of photons, electrons, and other atomic-scale objects.
The mathematical formulations of quantum mechanics are abstract. A mathematical function called the wavefunction provides information about the probability amplitude of position, momentum, and other physical properties of a particle. Mathematical manipulations of the wavefunction usually involve the bra-ket notation, which requires an understanding of complex numbers and linear functionals. The wavefunction treats the object as a quantum harmonic oscillator, and the mathematics is akin to that describing acoustic resonance. Many of the results of quantum mechanics are not easily visualized in terms of classical mechanics—for instance, the ground state in a quantum mechanical model is a non-zero energy state that is the lowest permitted energy state of a system, as opposed to a more "traditional" system that is thought of as simply being at rest, with zero kinetic energy. Instead of a traditional static, unchanging zero state, quantum mechanics allows for far more dynamic, chaotic possibilities, according to John Wheeler.
The earliest versions of quantum mechanics were formulated in the first decade of the 20th century. At around the same time, the atomic theory and the corpuscular theory of light (as updated by Einstein) first came to be widely accepted as scientific fact; these latter theories can be viewed as quantum theories of matter and electromagnetic radiation, respectively. Early quantum theory was significantly reformulated in the mid-1920s by Werner Heisenberg, Max Born and Pascual Jordan, who created matrix mechanics; Louis de Broglie and Erwin Schrödinger (Wave Mechanics); and Wolfgang Pauli and Satyendra Nath Bose (statistics of subatomic particles). And the Copenhagen interpretation of Niels Bohr became widely accepted. By 1930, quantum mechanics had been further unified and formalized by the work of David Hilbert, Paul Dirac and John von Neumann,[2] with a greater emphasis placed on measurement in quantum mechanics, the statistical nature of our knowledge of reality, and philosophical speculation about the role of the observer. Quantum mechanics has since branched out into almost every aspect of 20th century physics and other disciplines, such as quantum chemistry, quantum electronics, quantum optics, and quantum information science. Much 19th century physics has been re-evaluated as the "classical limit" of quantum mechanics, and its more advanced developments in terms of quantum field theory, string theory, and speculative quantum gravity theories.

Contents

History

Modern physics
{ i\hbar\frac{\partial}{\partial t} \Psi(\mathbf{r},\,t) = \hat H \Psi(\mathbf{r},\,t)}
History of modern physics
Main article: History of quantum mechanics
Scientific inquiry into the wave nature of light go back to the 17th and 18th centuries when scientists such as Robert Hooke, Christian Huygens and Leonhard Euler proposed a wave theory of light based on experimental observations.[3] In 1803, Thomas Young, an English polymath, performed the famous double-slit experiment that he later described in a paper entitled "On the nature of light and colours". This experiment played a major role in the general acceptance of the wave theory of light.
In 1838 with the discovery of cathode rays by Michael Faraday, these studies were followed by the 1859 statement of the black-body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system can be discrete, and the 1900 quantum hypothesis of Max Planck.[4] Planck's hypothesis that energy is radiated and absorbed in discrete "quanta" (or "energy elements") precisely matched the observed patterns of black-body radiation.
In 1896, Wilhelm Wien empirically determined a distribution law of black-body radiation, later named Wien's law after him. However, it was only valid at high frequencies, and underestimated the radiancy at low frequencies. Later Max Planck corrected the theory and proposed what is now called Planck's law, which led to the development of quantum mechanics.
The first studies of quantum phenomena in nature were by the work of several scientists as Arthur Compton, C.V. Raman, Pieter Zeeman (each one of them has a quantum effect named after their works), Albert Einstein and Robert A. Millikan (both studied the Photoelectric effect). At the same time Niels Bohr developed his theory of the atomic structure later confirmed with experiments by Henry Moseley. In 1913, Peter Debye extended Niels Bohr's theory of atomic structure, introducing elliptical orbits, a concept also introduced by Arnold Sommerfeld[5] . This phase is known as Old quantum theory.
According to Planck, each energy element E is proportional to its frequency ν:
E = h \nu\

Planck is considered the father of the Quantum Theory
where h is Planck's constant. Planck (cautiously) insisted that this was simply an aspect of the processes of absorption and emission of radiation and had nothing to do with the physical reality of the radiation itself.[6] However, in 1905 Albert Einstein interpreted Planck's quantum hypothesis realistically and used it to explain the photoelectric effect, in which shining light on certain materials can eject electrons from the material.

The 1927 Solvay Conference in Brussels.
The foundations of quantum mechanics were established during the first half of the 20th century by Max Planck, Niels Bohr, Werner Heisenberg, Louis de Broglie, Arthur Compton, Albert Einstein, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Enrico Fermi, Wolfgang Pauli, Max Von Laue, Freeman Dyson, David Hilbert, Wilhelm Wien, Satyendra Nath Bose, Arnold Sommerfeld and others. In the mid-1920s, developments in quantum mechanics led to its becoming the standard formulation for atomic physics. In the summer of 1925, Bohr and Heisenberg published results that closed the "Old Quantum Theory". Out of deference to their particle-like behavior in certain processes and measurements, light quanta came to be called photons (1926). From Einstein's simple postulation was born a flurry of debating, theorizing, and testing. Thus the entire field of quantum physics emerged, leading to its wider acceptance at the Fifth Solvay Conference in 1927.
The other exemplar that led to quantum mechanics was the study of electromagnetic waves, such as visible light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or "quanta", Albert Einstein further developed this idea to show that an electromagnetic wave such as light could be described as a particle (later called the photon) with a discrete quantum of energy that was dependent on its frequency.[7] This led to a theory of unity between subatomic particles and electromagnetic waves, called wave–particle duality, in which particles and waves were neither one nor the other, but had certain properties of both.
While quantum mechanics traditionally described the world of the very small, it is also needed to explain certain recently investigated macroscopic systems such as superconductors and superfluids.
The word quantum derives from the Latin, meaning "how great" or "how much".[8] In quantum mechanics, it refers to a discrete unit that quantum theory assigns to certain physical quantities, such as the energy of an atom at rest (see Figure 1). The discovery that particles are discrete packets of energy with wave-like properties led to the branch of physics dealing with atomic and sub-atomic systems which is today called quantum mechanics. It is the underlying mathematical framework of many fields of physics and chemistry, including condensed matter physics, solid-state physics, atomic physics, molecular physics, computational physics, computational chemistry, quantum chemistry, particle physics, nuclear chemistry, and nuclear physics.[9] Some fundamental aspects of the theory are still actively studied.[10]
Quantum mechanics is essential to understanding the behavior of systems at atomic length scales and smaller. For example, if classical mechanics truly governed the workings of an atom, electrons would rapidly travel toward, and collide with, the nucleus, making stable atoms impossible. However, in the natural world electrons normally remain in an uncertain, non-deterministic, "smeared", probabilistic wave–particle wavefunction orbital path around (or through) the nucleus, defying classical electromagnetism.[11]
Quantum mechanics was initially developed to provide a better explanation of the atom, especially the differences in the spectra of light emitted by different isotopes of the same element. The quantum theory of the atom was developed as an explanation for the electron remaining in its orbit, which could not be explained by Newton's laws of motion and Maxwell's laws of (classical) electromagnetism.
Broadly speaking, quantum mechanics incorporates four classes of phenomena for which classical physics cannot account:

Mathematical formulations

Main article: Mathematical formulations of quantum mechanics
See also: Quantum logic
In the mathematically rigorous formulation of quantum mechanics developed by Paul Dirac[12] David Hilbert,[13] John von Neumann,[14] and Hermann Weyl[15] the possible states of a quantum mechanical system are represented by unit vectors (called "state vectors"). Formally, these reside in a complex separable Hilbert space - variously called the "state space" or the "associated Hilbert space" of the system - that is well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projective space of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system - for example, the state space for position and momentum states is the space of square-integrable functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a maximally Hermitian (precisely: by a self-adjoint) linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can only attain those discrete eigenvalues.
In the formalism of quantum mechanics, the state of a system at a given time is described by a complex wave function, also referred to as state vector in a complex vector space.[16] This abstract mathematical object allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of conjugate variables, such as position and momentum, with accuracy. For instance, electrons may be considered (to a certain probability) to be located somewhere within a given region of space, but with their exact positions unknown. Contours of constant probability, often referred to as "clouds", may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. Heisenberg's uncertainty principle quantifies the inability to precisely locate the particle given its conjugate momentum.[17]
According to one interpretation, as the result of a measurement the wave function containing the probability information for a system collapses from a given initial state to a particular eigenstate. The possible results of a measurement are the eigenvalues of the operator representing the observable — which explains the choice of Hermitian operators, for which all the eigenvalues are real. The probability distribution of an observable in a given state can be found by computing the spectral decomposition of the corresponding operator. Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute.
The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr-Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Newer interpretations of quantum mechanics have been formulated that do away with the concept of "wavefunction collapse" (see, for example, the relative state interpretation). The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become entangled, so that the original quantum system ceases to exist as an independent entity. For details, see the article on measurement in quantum mechanics.[18]
Generally, quantum mechanics does not assign definite values. Instead, it makes a prediction using a probability distribution; that is, it describes the probability of obtaining the possible outcomes from measuring an observable. Often these results are skewed by many causes, such as dense probability clouds. Probability clouds are approximate, but better than the Bohr model, whereby electron location is given by a probability function, the wave function eigenvalue, such that the probability is the squared modulus of the complex amplitude, or quantum state nuclear attraction.[19][20] Naturally, these probabilities will depend on the quantum state at the "instant" of the measurement. Hence, uncertainty is involved in the value. There are, however, certain states that are associated with a definite value of a particular observable. These are known as eigenstates of the observable ("eigen" can be translated from German as meaning "inherent" or "characteristic").[21]
In the everyday world, it is natural and intuitive to think of everything (every observable) as being in an eigenstate. Everything appears to have a definite position, a definite momentum, a definite energy, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values of a particle's position and momentum (since they are conjugate pairs) or its energy and time (since they too are conjugate pairs); rather, it only provides a range of probabilities of where that particle might be given its momentum and momentum probability. Therefore, it is helpful to use different words to describe states having uncertain values and states having definite values (eigenstates). Usually, a system will not be in an eigenstate of the observable (particle) we are interested in. However, if one measures the observable, the wavefunction will instantaneously be an eigenstate (or "generalized" eigenstate) of that observable. This process is known as wavefunction collapse, a controversial and much-debated process[22] that involves expanding the system under study to include the measurement device. If one knows the corresponding wave function at the instant before the measurement, one will be able to compute the probability of the wavefunction collapsing into each of the possible eigenstates. For example, the free particle in the previous example will usually have a wavefunction that is a wave packet centered around some mean position x0 (neither an eigenstate of position nor of momentum). When one measures the position of the particle, it is impossible to predict with certainty the result.[18] It is probable, but not certain, that it will be near x0, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result x, the wave function collapses into a position eigenstate centered at x.[23]
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian (the operator corresponding to the total energy of the system) generates the time evolution. The time evolution of wave functions is deterministic in the sense that - given a wavefunction at an initial time - it makes a definite prediction of what the wavefunction will be at any later time.[24]
During a measurement, on the other hand, the change of the initial wavefunction into another, later wavefunction is not deterministic, it is unpredictable (i.e. random). A time-evolution simulation can be seen here.[25][26]
Wave functions change as time progresses. The Schrödinger equation describes how wavefunctions change in time, playing a role similar to Newton's second law in classical mechanics. The Schrödinger equation, applied to the aforementioned example of the free particle, predicts that the center of a wave packet will move through space at a constant velocity (like a classical particle with no forces acting on it). However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain with time. This also has the effect of turning a position eigenstate (which can be thought of as an infinitely sharp wave packet) into a broadened wave packet that no longer represents a (definite, certain) position eigenstate.[27]

Fig. 1: Probability densities corresponding to the wavefunctions of an electron in a hydrogen atom possessing definite energy levels (increasing from the top of the image to the bottom: n = 1, 2, 3, ...) and angular momenta (increasing across from left to right: s, p, d, ...). Brighter areas correspond to higher probability density in a position measurement. Wavefunctions like these are directly comparable to Chladni's figures of acoustic modes of vibration in classical physics, and are indeed modes of oscillation as well, possessing a sharp energy and, thus, a definite frequency. The angular momentum and energy are quantized, and take only discrete values like those shown (as is the case for resonant frequencies in acoustics)
Some wave functions produce probability distributions that are constant, or independent of time - such as when in a stationary state of constant energy, time vanishes in the absolute square of the wave function. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics it is described by a static, spherically symmetric wavefunction surrounding the nucleus (Fig. 1) (note, however, that only the lowest angular momentum states, labeled s, are spherically symmetric).[28]
The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its phase encodes information about the interference between quantum states. This gives rise to the "wave-like" behavior of quantum states. As it turns out, analytic solutions of the Schrödinger equation are only available for a very small number of relatively simple model Hamiltonians, of which the quantum harmonic oscillator, the particle in a box, the hydrogen molecular ion, and the hydrogen atom are the most important representatives. Even the helium atom - which contains just one more electron than does the hydrogen atom - has defied all attempts at a fully analytic treatment.
There exist several techniques for generating approximate solutions, however. In the important method known as perturbation theory, one uses the analytic result for a simple quantum mechanical model to generate a result for a more complicated model that is related to the simpler model by (for one example) the addition of a weak potential energy. Another method is the "semi-classical equation of motion" approach, which applies to systems for which quantum mechanics produces only weak (small) deviations from classical behavior. These deviations can then be computed based on the classical motion. This approach is particularly important in the field of quantum chaos.

Mathematically equivalent formulations of quantum mechanics

There are numerous mathematically equivalent formulations of quantum mechanics. One of the oldest and most commonly used formulations is the "transformation theory" proposed by the late Cambridge theoretical physicist Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics - matrix mechanics (invented by Werner Heisenberg)[29] and wave mechanics (invented by Erwin Schrödinger).[30]
Especially since Werner Heisenberg was awarded the Nobel Prize in Physics in 1932 for the creation of quantum mechanics, the role of Max Born in the development of QM has become somewhat confused and overlooked. A 2005 biography of Born details his role as the creator of the matrix formulation of quantum mechanics. This fact was recognized in a paper that Heisenberg himself published in 1940 honoring Max Planck.[31] and In the matrix formulation, the instantaneous state of a quantum system encodes the probabilities of its measurable properties, or "observables". Examples of observables include energy, position, momentum, and angular momentum. Observables can be either continuous (e.g., the position of a particle) or discrete (e.g., the energy of an electron bound to a hydrogen atom).[32] An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over all possible histories between the initial and final states. This is the quantum-mechanical counterpart of the action principle in classical mechanics.

Interactions with other scientific theories

The rules of quantum mechanics are fundamental. They assert that the state space of a system is a Hilbert space, and that observables of that system are Hermitian operators acting on that space—although they do not tell us which Hilbert space or which operators. These can be chosen appropriately in order to obtain a quantitative description of a quantum system. An important guide for making these choices is the correspondence principle, which states that the predictions of quantum mechanics reduce to those of classical mechanics when a system moves to higher energies or—equivalently—larger quantum numbers, i.e. whereas a single particle exhibits a degree of randomness, in systems incorporating millions of particles averaging takes over and, at the high energy limit, the statistical probability of random behaviour approaches zero. In other words, classical mechanics is simply a quantum mechanics of large systems. This "high energy" limit is known as the classical or correspondence limit. One can even start from an established classical model of a particular system, then attempt to guess the underlying quantum model that would give rise to the classical model in the correspondence limit.
List of unsolved problems in physics
In the correspondence limit of quantum mechanics: Is there a preferred interpretation of quantum mechanics? How does the quantum description of reality, which includes elements such as the "superposition of states" and "wavefunction collapse", give rise to the reality we perceive?
When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.
Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein-Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field (rather than a fixed set of particles). The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction. The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one that has been employed since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical 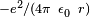\scriptstyle -e^2/(4 \pi\ \epsilon_{_0}\ r) Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Quantum field theories for the strong nuclear force and the weak nuclear force have also been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of subnuclear particles such as quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory (known as electroweak theory), by the physicists Abdus Salam, Sheldon Glashow and Steven Weinberg. These three men shared the Nobel Prize in Physics in 1979 for this work.[33]
It has proven difficult to construct quantum models of gravity, the remaining fundamental force. Semi-classical approximations are workable, and have led to predictions such as Hawking radiation. However, the formulation of a complete theory of quantum gravity is hindered by apparent incompatibilities between general relativity (the most accurate theory of gravity currently known) and some of the fundamental assumptions of quantum theory. The resolution of these incompatibilities is an area of active research, and theories such as string theory are among the possible candidates for a future theory of quantum gravity.
Classical mechanics has also been extended into the complex domain, with complex classical mechanics exhibiting behaviors similar to quantum mechanics.[34]

Quantum mechanics and classical physics

Predictions of quantum mechanics have been verified experimentally to an extremely high degree of accuracy. According to the correspondence principle between classical and quantum mechanics, all objects obey the laws of quantum mechanics, and classical mechanics is just an approximation for large systems of objects (or a statistical quantum mechanics of a large collection of particles). The laws of classical mechanics thus follow from the laws of quantum mechanics as a statistical average at the limit of large systems or large quantum numbers.[35] However, chaotic systems do not have good quantum numbers, and quantum chaos studies the relationship between classical and quantum descriptions in these systems.
Quantum coherence is an essential difference between classical and quantum theories, and is illustrated by the Einstein-Podolsky-Rosen paradox. Quantum interference involves adding together probability amplitudes, whereas classical "waves" infer that there is an adding together of intensities. For microscopic bodies, the extension of the system is much smaller than the coherence length, which gives rise to long-range entanglement and other nonlocal phenomena that are characteristic of quantum systems.[36] Quantum coherence is not typically evident at macroscopic scales - although an exception to this rule can occur at extremely low temperatures (i.e. approaching absolute zero), when quantum behavior can manifest itself on more macroscopic scales (see macroscopic quantum phenomena, Bose-Einstein condensate, and Quantum machine). This is in accordance with the following observations:
  • Many macroscopic properties of a classical system are a direct consequence of the quantum behavior of its parts. For example, the stability of bulk matter (which consists of atoms and molecules which would quickly collapse under electric forces alone), the rigidity of solids, and the mechanical, thermal, chemical, optical and magnetic properties of matter are all results of the interaction of electric charges under the rules of quantum mechanics.[37]
  • While the seemingly "exotic" behavior of matter posited by quantum mechanics and relativity theory become more apparent when dealing with particles of extremely small size or velocities approaching the speed of light, the laws of classical Newtonian physics remain accurate in predicting the behavior of the vast majority of "large" objects (on the order of the size of large molecules or bigger) at velocities much smaller than the velocity of light.[38]

Relativity and quantum mechanics

Main articles: Quantum gravity and Theory of everything
Even with the defining postulates of both Einstein's theory of general relativity and quantum theory being indisputably supported by rigorous and repeated empirical evidence and while they do not directly contradict each other theoretically (at least with regard to their primary claims), they have proven extremely difficult to incorporate into one consistent, cohesive model.[39]
Einstein himself is well known for rejecting some of the claims of quantum mechanics. While clearly contributing to the field, he did not accept many of the more "philosophical consequences and interpretations" of quantum mechanics, such as the lack of deterministic causality. He is famously quoted as saying, in response to this aspect, "My God does not play with dice". He also had difficulty with the assertion that a single subatomic particle can occupy numerous areas of space at one time. However, he was also the first to notice some of the apparently exotic consequences of entanglement, and used them to formulate the Einstein-Podolsky-Rosen paradox in the hope of showing that quantum mechanics had unacceptable implications. This was 1935, but in 1964 it was shown by John Bell (see Bell inequality) that - although Einstein was correct in identifying seemingly paradoxical implications of quantum mechanical nonlocality - these implications could be experimentally tested. Alain Aspect's initial experiments in 1982, and many subsequent experiments since, have definitively verified quantum entanglement.
According to the paper of J. Bell and the Copenhagen interpretation - the common interpretation of quantum mechanics by physicists since 1927 - and contrary to Einstein's ideas, quantum mechanics was not, at the same time:
  • a "realistic" theory
and
The Einstein-Podolsky-Rosen paradox shows in any case that there exist experiments by which one can measure the state of one particle and instantaneously change the state of its entangled partner - although the two particles can be an arbitrary distance apart. However, this effect does not violate causality, since no transfer of information happens. Quantum entanglement forms the basis of quantum cryptography, which is used in high-security commercial applications in banking and government.
Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those particular applications. However, the lack of a correct theory of quantum gravity is an important issue in cosmology and the search by physicists for an elegant "Theory of Everything" (TOE). Consequently, resolving the inconsistencies between both theories has been a major goal of 20th and 21st century physics. Many prominent physicists, including Stephen Hawking, have labored for many years in the attempt to discover a theory underlying everything. This TOE would combine not only the different models of subatomic physics, but also derive the four fundamental forces of nature - the strong force, electromagnetism, the weak force, and gravity - from a single force or phenomenon. While Stephen Hawking was initially a believer in the Theory of Everything, after considering Gödel's Incompleteness Theorem, he has concluded that one is not obtainable, and has stated so publicly in his lecture "Gödel and the End of Physics" (2002).[40]

Attempts at a unified field theory

Main article: Grand unified theory
The quest to unify the fundamental forces through quantum mechanics is still ongoing. Quantum electrodynamics (or "quantum electromagnetism"), which is currently (in the perturbative regime at least) the most accurately tested physical theory,[41][unreliable source](blog) has been successfully merged with the weak nuclear force into the electroweak force and work is currently being done to merge the electroweak and strong force into the electrostrong force. Current predictions state that at around 1014 GeV the three aforementioned forces are fused into a single unified field,[42] Beyond this "grand unification," it is speculated that it may be possible to merge gravity with the other three gauge symmetries, expected to occur at roughly 1019 GeV. However — and while special relativity is parsimoniously incorporated into quantum electrodynamics — the expanded general relativity, currently the best theory describing the gravitation force, has not been fully incorporated into quantum theory. One of the leading authorities continuing the search for a coherent TOE is Edward Witten, a theoretical physicist who formulated the groundbreaking M-theory, which is an attempt at describing the supersymmetrical based string theory. M-theory posits that our apparent 4-dimensional spacetime is, in reality, actually an 11-dimensional spacetime containing 10 spatial dimensions and 1 time dimension, although 7 of the spatial dimensions are - at lower energies - completely "compactified" (or infinitely curved) and not readily amenable to measurement or probing.
Other popular theory is Loop quantum gravity (LQG) a theory that describes the quantum properties of gravity. It is also a theory of quantum space and quantum time, because, as discovered with general relativity, the geometry of spacetime is a manifestation of gravity. LQG is an attempt to merge and adapt standard quantum mechanics and standard general relativity. The main output of the theory is a physical picture of space where space is granular. The granularity is a direct consequence of the quantization. It has the same nature of the granularity of the photons in the quantum theory of electromagnetism or the discrete levels of the energy of the atoms. But here it is space itself which is discrete. More precisely, space can be viewed as an extremely fine fabric or network "woven" of finite loops. These networks of loops are called spin networks. The evolution of a spin network over time, is called a spin foam. The predicted size of this structure is the Planck length, which is approximately 1.616×10−35 m. According to theory, there is no meaning to length shorter than this (cf. Planck scale energy). Therefore LQG predicts that not just matter, but also space itself, has an atomic structure. Loop quantum Gravity was first proposed by Carlo Rovelli.

Philosophical implications

Main article: Interpretations of quantum mechanics
Since its inception, the many counter-intuitive aspects and results of quantum mechanics have provoked strong philosophical debates and many interpretations. Even fundamental issues, such as Max Born's basic rules concerning probability amplitudes and probability distributions took decades to be appreciated by society and many leading scientists. Indeed, the renowned physicist Richard Feynman once said, "I think I can safely say that nobody understands quantum mechanics."[43]
The Copenhagen interpretation - due largely to the Danish theoretical physicist Niels Bohr - remains the quantum mechanical formalism that is currently most widely accepted amongst physicists, some 75 years after its enunciation. According to this interpretation, the probabilistic nature of quantum mechanics is not a temporary feature which will eventually be replaced by a deterministic theory, but instead must be considered a final renunciation of the classical idea of "causality". It is also believed therein that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement, due to the complementarity nature of evidence obtained under different experimental situations.
Albert Einstein, himself one of the founders of quantum theory, disliked this loss of determinism in measurement. Einstein held that there should be a local hidden variable theory underlying quantum mechanics and, consequently, that the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the Einstein-Podolsky-Rosen paradox. John Bell showed that this "EPR" paradox led to experimentally testable differences between quantum mechanics and local realistic theories. Experiments have been performed confirming the accuracy of quantum mechanics, thereby demonstrating that the physical world cannot be described by any local realistic theory.[44] The Bohr-Einstein debates provide a vibrant critique of the Copenhagen Interpretation from an epistemological point of view.
The Everett many-worlds interpretation, formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a multiverse composed of mostly independent parallel universes.[45] This is not accomplished by introducing some "new axiom" to quantum mechanics, but on the contrary, by removing the axiom of the collapse of the wave packet. All of the possible consistent states of the measured system and the measuring apparatus (including the observer) are present in a real physical - not just formally mathematical, as in other interpretations - quantum superposition. Such a superposition of consistent state combinations of different systems is called an entangled state. While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we can observe only the universe (i.e., the consistent state contribution to the aforementioned superposition) that we, as observers, inhabit. Everett's interpretation is perfectly consistent with John Bell's experiments and makes them intuitively understandable. However, according to the theory of quantum decoherence, these "parallel universes" will never be accessible to us. The inaccessibility can be understood as follows: once a measurement is done, the measured system becomes entangled with both the physicist who measured it and a huge number of other particles, some of which are photons flying away at the speed of light towards the other end of the universe. In order to prove that the wave function did not collapse, one would have to bring all these particles back and measure them again, together with the system that was originally measured. Not only is this completely impractical, but even if one could theoretically do this, it would destroy any evidence that the original measurement took place (to include the physicist's memory).[citation needed] In light of these Bell tests, Cramer (1986) formulated his Transactional interpretation.[46] Relational quantum mechanics appeared in the late 1990s as the modern derivative of the Copenhagen Interpretation.

Applications

Quantum mechanics had enormous[47] success in explaining many of the features of our world. The individual behaviors of the subatomic particles that make up all forms of matter (electrons, protons, neutrons, photons, and others) can often only be satisfactorily described using quantum mechanics. Quantum mechanics has strongly influenced string theories, candidates for a Theory of Everything (see reductionism), and the multiverse hypotheses.
Quantum mechanics is also critically important for understanding how individual atoms combine covalently to form molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. Relativistic quantum mechanics can, in principle, mathematically describe most of chemistry. Quantum mechanics can also provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which others, and the magnitudes of the energies involved.[48] Furthermore, most of the calculations performed in modern computational chemistry rely on quantum mechanics.

A working mechanism of a resonant tunneling diode device, based on the phenomenon of quantum tunneling through potential barriers
A great deal of modern technological inventions operate at a scale where quantum effects are significant. Examples include the laser, the transistor (and thus the microchip), the electron microscope, and magnetic resonance imaging (MRI). The study of semiconductors led to the invention of the diode and the transistor, which are indispensable parts of modern electronics systems and devices.
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to more fully develop quantum cryptography, which will theoretically allow guaranteed secure transmission of information. A more distant goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Another active research topic is quantum teleportation, which deals with techniques to transmit quantum information over arbitrary distances.
Quantum tunneling is vital to the operation of many devices - even in the simple light switch, as otherwise the electrons in the electric current could not penetrate the potential barrier made up of a layer of oxide. Flash memory chips found in USB drives use quantum tunneling to erase their memory cells.
While quantum mechanics primarily applies to the atomic regimes of matter and energy, some systems exhibit quantum mechanical effects on a large scale - superfluidity, the frictionless flow of a liquid at temperatures near absolute zero, is one well-known example. Quantum theory also provides accurate descriptions for many previously unexplained phenomena, such as black body radiation and the stability of the orbitals of electrons in atoms. It has also given insight into the workings of many different biological systems, including smell receptors and protein structures.[49] Recent work on photosynthesis has provided evidence that quantum correlations play an essential role in this basic fundamental process of the plant kingdom.[50] Even so, classical physics can often provide good approximations to results otherwise obtained by quantum physics, typically in circumstances with large numbers of particles or large quantum numbers.

Examples

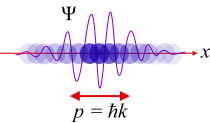
Free particle

For example, consider a free particle. In quantum mechanics, there is wave-particle duality, so the properties of the particle can be described as the properties of a wave. Therefore, its quantum state can be represented as a wave of arbitrary shape and extending over space as a wave function. The position and momentum of the particle are observables. The Uncertainty Principle states that both the position and the momentum cannot simultaneously be measured with complete precision. However, one can measure the position (alone) of a moving free particle, creating an eigenstate of position with a wavefunction that is very large (a Dirac delta) at a particular position x, and zero everywhere else. If one performs a position measurement on such a wavefunction, the resultant x will be obtained with 100% probability (i.e., with full certainty, or complete precision). This is called an eigenstate of position—or, stated in mathematical terms, a generalized position eigenstate (eigendistribution). If the particle is in an eigenstate of position, then its momentum is completely unknown. On the other hand, if the particle is in an eigenstate of momentum, then its position is completely unknown.[51] In an eigenstate of momentum having a plane wave form, it can be shown that the wavelength is equal to h/p, where h is Planck's constant and p is the momentum of the eigenstate.[52]

3D confined electron wave functions for each eigenstate in a Quantum Dot. Here, rectangular and triangular-shaped quantum dots are shown. Energy states in rectangular dots are more ‘s-type’ and ‘p-type’. However, in a triangular dot, the wave functions are mixed due to confinement symmetry.

Step potential

Main article: Solution of Schrödinger equation for a step potential

Scattering at a finite potential step of height V0, shown in green. The amplitudes and direction of left- and right-moving waves are indicated. Yellow is the incident wave, blue are reflected and transmitted waves, red does not occur. E > V0 for this figure.
The potential in this case is given by:
V(x)= \begin{cases} 0, & x < 0, \\ V_0, & x \ge 0. \end{cases}
The solutions are superpositions of left- and right-moving waves:
\psi_1(x)= \frac{1}{\sqrt{k_1}} \left(A_\rightarrow e^{i k_1 x} + A_\leftarrow e^{-ik_1x}\right)\quad x<0 ,
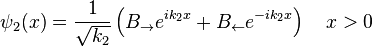
\psi_2(x)= \frac{1}{\sqrt{k_2}} \left(B_\rightarrow e^{i k_2 x} + B_\leftarrow e^{-ik_2x}\right)\quad x>0
where the wave vectors are related to the energy via
k_1=\sqrt{2m E/\hbar^2}, and
k_2=\sqrt{2m (E-V_0)/\hbar^2}
and the coefficients A and B are determined from the boundary conditions and by imposing a continuous derivative on the solution.
Each term of the solution can be interpreted as an incident, reflected, or transmitted component of the wave, allowing the calculation of transmission and reflection coefficients. In contrast to classical mechanics, incident particles with energies higher than the size of the potential step are still partially reflected.

Rectangular potential barrier

Main article: Rectangular potential barrier
This is a model for the quantum tunneling effect, which has important applications to modern devices such as flash memory and the scanning tunneling microscope.

Particle in a box


1-dimensional potential energy box (or infinite potential well)
Main article: Particle in a box
The particle in a one-dimensional potential energy box is the most simple example where restraints lead to the quantization of energy levels. The box is defined as having zero potential energy everywhere inside a certain region, and infinite potential energy everywhere outside' that region. For the one-dimensional case in the x direction, the time-independent Schrödinger equation can be written as:[53]
- \frac {\hbar ^2}{2m} \frac {d ^2 \psi}{dx^2} = E \psi.
Writing the differential operator
\hat{p}_x = -i\hbar\frac{d}{dx}
the previous equation can be seen to be evocative of the classic kinetic energy analogue
\frac{1}{2m} \hat{p}_x^2 = E
with E as the energy for the state \psi, which in this case coincides with the kinetic energy of the particle.
The general solutions of the Schrödinger equation for the particle in a box are:
\psi(x) = A e^{ikx} + B e ^{-ikx} \qquad\qquad E = \frac{\hbar^2 k^2}{2m}
or, from Euler's formula,
\psi(x) = C \sin kx + D \cos kx.\!
The presence of the walls of the box determines the values of C, D, and k. At each wall (x = 0 and x = L), ψ = 0. Thus when x = 0,
\psi(0) = 0 = C\sin 0 + D\cos 0 = D\!
and so D = 0. When x = L,
\psi(L) = 0 = C\sin kL.\!
C cannot be zero, since this would conflict with the Born interpretation. Therefore, sin kL = 0, and so it must be that kL is an integer multiple of π. And additionally,
k = \frac{n\pi}{L}\qquad\qquad n=1,2,3,\ldots.
The quantization of energy levels follows from this constraint on k, since
E = \frac{\hbar^2 \pi^2 n^2}{2mL^2} = \frac{n^2h^2}{8mL^2}.

Finite potential well

Main article: Finite potential well
This is the generalization of the infinite potential well problem to potential wells of finite depth.

Harmonic oscillator

Main article: Quantum harmonic oscillator

Some trajectories of a harmonic oscillator (i.e. a ball attached to a spring) in classical mechanics (A-B) and quantum mechanics (C-H). In quantum mechanics, the position of the ball is represented by a wave (called the wavefunction), with the real part shown in blue and the imaginary part shown in red. Some of the trajectories (such as C,D,E,and F) are standing waves (or "stationary states"). Each standing-wave frequency is proportional to a possible energy level of the oscillator. This "energy quantization" does not occur in classical physics, where the oscillator can have any energy.
As in the classical case, the potential for the quantum harmonic oscillator is given by:
V(x)=\frac{1}{2}m\omega^2x^2
This problem can be solved either by solving the Schrödinger equation directly, which is not trivial, or by using the more elegant "ladder method", first proposed by Paul Dirac. The eigenstates are given by:
\psi_n(x) = \sqrt{\frac{1}{2^n\,n!}} \cdot \left(\frac{m\omega}{\pi \hbar}\right)^{1/4} \cdot e^{ - \frac{m\omega x^2}{2 \hbar}} \cdot H_n\left(\sqrt{\frac{m\omega}{\hbar}} x \right), \qquad n = 0,1,2,\ldots.
where Hn are the Hermite polynomials:
H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}\left(e^{-x^2}\right)
and the corresponding energy levels are
E_n = \hbar \omega \left(n + {1\over 2}\right).
This is another example which illustrates the quantization of energy for bound states.

See also

Portal iconPhysics portal

Notes

  1. ^ The angular momentum of an unbound electron, in contrast, is not quantized.
  2. ^ van Hove, Leon (1958). "Von Neumann's contributions to quantum mechanics" (PDF). Bulletin of the American Mathematical Society 64: Part2:95–99. http://www.ams.org/journals/bull/1958-64-03/S0002-9904-1958-10206-2/S0002-9904-1958-10206-2.pdf.
  3. ^ Max Born & Emil Wolf, Principles of Optics, 1999, Cambridge University Press
  4. ^ Mehra, J.; Rechenberg, H. (1982). The historical development of quantum theory. New York: Springer-Verlag. ISBN 0387906428.
  5. ^ http://www.ias.ac.in/resonance/December2010/p1056-1059.pdf
  6. ^ Kuhn, T. S. (1978). Black-body theory and the quantum discontinuity 1894-1912. Oxford: Clarendon Press. ISBN 0195023838.
  7. ^ Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt [On a heuristic point of view concerning the production and transformation of light]". Annalen der Physik 17 (6): 132–148. Bibcode 1905AnP...322..132E. doi:10.1002/andp.19053220607. Reprinted in The collected papers of Albert Einstein, John Stachel, editor, Princeton University Press, 1989, Vol. 2, pp. 149-166, in German; see also Einstein's early work on the quantum hypothesis, ibid. pp. 134-148.
  8. ^ "Quantum - Definition and More from the Free Merriam-Webster Dictionary". Merriam-webster.com. http://www.merriam-webster.com/dictionary/quantum. Retrieved 2012-08-18.
  9. ^ http://mooni.fccj.org/~ethall/quantum/quant.htm
  10. ^ Compare the list of conferences presented here
  11. ^ Oocities.com at the Wayback Machine (archived October 26, 2009)[dead link]
  12. ^ P.A.M. Dirac, The Principles of Quantum Mechanics, Clarendon Press, Oxford, 1930.
  13. ^ D. Hilbert Lectures on Quantum Theory, 1915-1927
  14. ^ J. von Neumann, Mathematische Grundlagen der Quantenmechanik, Springer, Berlin, 1932 (English translation: Mathematical Foundations of Quantum Mechanics, Princeton University Press, 1955).
  15. ^ H.Weyl "The Theory of Groups and Quantum Mechanics", 1931 (original title:"Gruppentheorie una Quantenmechanik").
  16. ^ Greiner, Walter; Müller, Berndt (1994). Quantum Mechanics Symmetries, Second edition. Springer-Verlag. p. 52. ISBN 3-540-58080-8. http://books.google.com/books?id=gCfvWx6vuzUC&pg=PA52., Chapter 1, p. 52
  17. ^ "Heisenberg - Quantum Mechanics, 1925-1927: The Uncertainty Relations". Aip.org. http://www.aip.org/history/heisenberg/p08a.htm. Retrieved 2012-08-18.
  18. ^ a b Greenstein, George; Zajonc, Arthur (2006). The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics, Second edition. Jones and Bartlett Publishers, Inc. p. 215. ISBN 0-7637-2470-X. http://books.google.com/books?id=5t0tm0FB1CsC&pg=PA215., Chapter 8, p. 215
  19. ^ "[Abstract] Visualization of Uncertain Particle Movement". Actapress.com. http://www.actapress.com/PaperInfo.aspx?PaperID=25988&reason=500. Retrieved 2012-08-18.
  20. ^ Hirshleifer, Jack (2001). The Dark Side of the Force: Economic Foundations of Conflict Theory. Campbridge University Press. p. 265. ISBN 0-521-80412-4. http://books.google.com/books?id=W2J2IXgiZVgC&pg=PA265., Chapter , p.
  21. ^ Dict.cc
    De.pons.eu
  22. ^ "Topics: Wave-Function Collapse". Phy.olemiss.edu. 2012-07-27. http://www.phy.olemiss.edu/~luca/Topics/qm/collapse.html. Retrieved 2012-08-18.
  23. ^ "Collapse of the wave-function". Farside.ph.utexas.edu. http://farside.ph.utexas.edu/teaching/qmech/lectures/node28.html. Retrieved 2012-08-18.
  24. ^ "Determinism and Naive Realism : philosophy". Reddit.com. 2009-06-01. http://www.reddit.com/r/philosophy/comments/8p2qv/determinism_and_naive_realism/. Retrieved 2012-08-18.
  25. ^ Michael Trott. "Time-Evolution of a Wavepacket in a Square Well — Wolfram Demonstrations Project". Demonstrations.wolfram.com. http://demonstrations.wolfram.com/TimeEvolutionOfAWavepacketInASquareWell/. Retrieved 2010-10-15.
  26. ^ Michael Trott. "Time Evolution of a Wavepacket In a Square Well". Demonstrations.wolfram.com. http://demonstrations.wolfram.com/TimeEvolutionOfAWavepacketInASquareWell/. Retrieved 2010-10-15.
  27. ^ Mathews, Piravonu Mathews; Venkatesan, K. (1976). A Textbook of Quantum Mechanics. Tata McGraw-Hill. p. 36. ISBN 0-07-096510-2. http://books.google.com/books?id=_qzs1DD3TcsC&pg=PA36., Chapter 2, p. 36
  28. ^ "Wave Functions and the Schrödinger Equation" (PDF). http://physics.ukzn.ac.za/~petruccione/Phys120/Wave%20Functions%20and%20the%20Schr%F6dinger%20Equation.pdf. Retrieved 2010-10-15.[dead link]
  29. ^ "Quantum Physics: Werner Heisenberg Uncertainty Principle of Quantum Mechanics. Werner Heisenberg Biography". Spaceandmotion.com. 1976-02-01. http://www.spaceandmotion.com/physics-quantum-mechanics-werner-heisenberg.htm. Retrieved 2012-08-18.
  30. ^ http://th-www.if.uj.edu.pl/acta/vol19/pdf/v19p0683.pdf
  31. ^ Nancy Thorndike Greenspan, "The End of the Certain World: The Life and Science of Max Born" (Basic Books, 2005), pp. 124-8 and 285-6.
  32. ^ http://ocw.usu.edu/physics/classical-mechanics/pdf_lectures/06.pdf
  33. ^ "The Nobel Prize in Physics 1979". Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1979/index.html. Retrieved 2010-02-16.
  34. ^ Carl M. Bender, Daniel W. Hook, Karta Kooner (2009-12-31). "Complex Elliptic Pendulum". arXiv:1001.0131 [hep-th].
  35. ^ "Quantum mechanics course iwhatisquantummechanics". Scribd.com. 2008-09-14. http://www.scribd.com/doc/5998949/Quantum-mechanics-course-iwhatisquantummechanics. Retrieved 2012-08-18.
  36. ^ "Between classical and quantum�" (PDF). http://philsci-archive.pitt.edu/2328/1/handbook.pdf. Retrieved 2012-08-19.
  37. ^ "Atomic Properties". Academic.brooklyn.cuny.edu. http://academic.brooklyn.cuny.edu/physics/sobel/Nucphys/atomprop.html. Retrieved 2012-08-18.
  38. ^ http://assets.cambridge.org/97805218/29526/excerpt/9780521829526_excerpt.pdf
  39. ^ "There is as yet no logically consistent and complete relativistic quantum field theory.", p. 4. — V. B. Berestetskii, E. M. Lifshitz, L P Pitaevskii (1971). J. B. Sykes, J. S. Bell (translators). Relativistic Quantum Theory 4, part I. Course of Theoretical Physics (Landau and Lifshitz) ISBN 0-08-016025-5
  40. ^ http://www.damtp.cam.ac.uk/strings02/dirac/hawking/
  41. ^ "Life on the lattice: The most accurate theory we have". Latticeqcd.blogspot.com. 2005-06-03. http://latticeqcd.blogspot.com/2005/06/most-accurate-theory-we-have.html. Retrieved 2010-10-15.
  42. ^ Parker, B. (1993). Overcoming some of the problems. pp. 259–279.
  43. ^ The Character of Physical Law (1965) Ch. 6; also quoted in The New Quantum Universe (2003), by Tony Hey and Patrick Walters
  44. ^ "Action at a Distance in Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. 2007-01-26. http://plato.stanford.edu/entries/qm-action-distance/. Retrieved 2012-08-18.
  45. ^ "Everett's Relative-State Formulation of Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. http://plato.stanford.edu/entries/qm-everett/. Retrieved 2012-08-18.
  46. ^ The Transactional Interpretation of Quantum Mechanics by John Cramer. Reviews of Modern Physics 58, 647-688, July (1986)
  47. ^ See, for example, the Feynman Lectures on Physics for some of the technological applications which use quantum mechanics, e.g., transistors (vol III, pp. 14-11 ff), integrated circuits, which are follow-on technology in solid-state physics (vol II, pp. 8-6), and lasers (vol III, pp. 9-13).
  48. ^ Introduction to Quantum Mechanics with Applications to Chemistry - Linus Pauling, E. Bright Wilson. Books.google.com. 1985-03-01. ISBN 9780486648712. http://books.google.com/books?id=vdXU6SD4_UYC. Retrieved 2012-08-18.
  49. ^ Anderson, Mark (2009-01-13). "Is Quantum Mechanics Controlling Your Thoughts? | Subatomic Particles". DISCOVER Magazine. http://discovermagazine.com/2009/feb/13-is-quantum-mechanics-controlling-your-thoughts/article_view?b_start:int=1&-C. Retrieved 2012-08-18.
  50. ^ "Quantum mechanics boosts photosynthesis". physicsworld.com. http://physicsworld.com/cws/article/news/41632. Retrieved 2010-10-23.
  51. ^ Davies, P. C. W.; Betts, David S. (1984). Quantum Mechanics, Second edition. Chapman and Hall. p. 79. ISBN 0-7487-4446-0. http://books.google.com/books?id=XRyHCrGNstoC&pg=PA79., Chapter 6, p. 79
  52. ^ Baofu, Peter (2007-12-31). The Future of Complexity: Conceiving a Better Way to Understand Order and Chaos. Books.google.com. ISBN 9789812708991. http://books.google.com/books?id=tKm-Ekwke_UC. Retrieved 2012-08-18.
  53. ^ Derivation of particle in a box, chemistry.tidalswan.com

References

The following titles, all by working physicists, attempt to communicate quantum theory to lay people, using a minimum of technical apparatus.
More technical:

Further reading

External links

Find more about Quantum mechanics at Wikipedia's sister projects
Definitions and translations from Wiktionary
Media from Commons
Learning resources from Wikiversity
News stories from Wikinews
Quotations from Wikiquote
Source texts from Wikisource
Textbooks from Wikibooks
Travel information from Wikivoyage
Course material
FAQs
Media
Philosophy
Branches of physics
Divisions
Energy and motion
Waves and fields
Physical sciences
and mathematics
Physics and biology /
geology / economics



Retrieved from "http://en.wikipedia.org/w/index.php?title=Quantum_mechanics&oldid=539186855"

-
Labels: , , , , ,

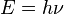
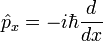
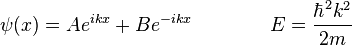
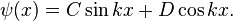
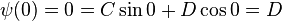
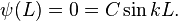
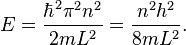
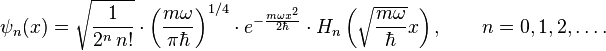
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)

The Mathematical Theory of Spirit by Stanley Redgrove, 1913

  A Mathematical Theory of Spirit: Being an Attempt to Employ Certain Mathematical Principles in the Elucidation of Some Metaphysical Proble...

  • The Multiverse
    https://wiki.p2pfoundation.net/Multi-Dimensional_Science From Wikipedia, the free encyclopedia Jump to navigation Jump to search ...
  • Quantum Mind
      From Wikipedia, the free encyclopedia Jump to navigation Jump to search Not to be confused with  Quantum cognition . The  quantum mind  or...
  • Signs of progress on the path of meditation
    Category: Meditation by Swami Sivananda Swami Sivananda Saraswati (Sep 8, 1887—Jul 14, 1963), was an Indian spiritual ...