Shape

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article is about describing the shape of an object. For common shapes, see list of geometric shapes. For other uses, see Shape (disambiguation).

The shape (Old English: gesceap, created thing) of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material composition.
Mathematician and statistician David George Kendall writes:^[1]

In this paper ‘shape’ is used in the vulgar sense, and means what one would normally expect it to mean. [...] We here define ‘shape’ informally as ‘all the geometrical information that remains when location, scale^[2] and rotational effects are filtered out from an object.’

Simple shapes can be described by basic geometry objects such as a set of two or more points, a line, a curve, a plane, a plane figure (e.g. square or circle), or a solid figure (e.g. cube or sphere). Most shapes occurring in the physical world are complex. Some, such as plant structures and coastlines, may be so arbitrary as to defy traditional mathematical description – in which case they may be analyzed by differential geometry, or as fractals.
== Rigid shape definition == nek minit

In geometry, two subsets of a Euclidean space have the same shape if one can be transformed to the other by a combination of translations, rotations (together also called rigid transformations), and uniform scalings. In other words, the shape of a set of points is all the geometrical information that is invariant to translations, rotations, and size changes. Having the same shape is an equivalence relation, and accordingly a precise mathematical definition of the notion of shape can be given as being an equivalence class of subsets of a Euclidean space having the same shape.
Shapes of physical objects are equal if the subsets of space these objects occupy satisfy the definition above. In particular, the shape does not depend on the size and placement in space of the object. For instance, a "p" and a "d" have the same shape, as they can be perfectly superimposed if the "p" is translated to the right by a given distance, rotated upside down and magnified by a given factor (see Procrustes superimposition for details). However, a mirror image could be called a different shape. For instance, a "b" and a "d" have a different shape, at least when they are constrained to move within a two-dimensional space like the page on which they are written. Even though they have the same size, there's no way to perfectly superimpose them by traslating and rotating them along the page. Similarly, within a three-dimensional space, a right hand and a left hand have a different shape, even if they are the mirror images of each other. Shapes may change if the object is scaled non uniformly. For example, a sphere becomes an ellipsoid when scaled differently in the vertical and horizontal directions. In other words, preserving axes of symmetry (if they exist) is important for preserving shapes. Also, shape is determined by only the outer boundary of an object. For example, a solid ice cube and a second ice cube containing an inner cavity (air bubble) have the same shape.^{[citation needed]}
Objects that can be transformed into each other by rigid transformations and mirroring are congruent. An object is therefore congruent to its mirror image (even if it is not symmetric), but not to a scaled version. Objects that have the same shape or one has the same shape as the other's mirror image (or both if they are themselves symmetric) are called geometrically similar. Thus congruent objects are always geometrically similar, but geometrical similarity additionally allows uniform scaling.

Contents  [hide]  1 Non-rigid shape definition 2 Colloquial shape definition 3 Philosophical skepticism of definitions 4 Shape analysis 5 Similarity classes 6 References 7 External links

[edit] Non-rigid shape definition

A more flexible definition of shape takes into consideration the fact that realistic shapes are often deformable, e.g. a person in different postures, a tree bending in the wind or a hand with different finger positions. By allowing also isometric (or near-isometric) deformations like bending, the intrinsic geometry of the object will stay the same, while sub-parts might be located at very different positions in space. This definition uses the fact that, geodesics (curves measured along the surface of the object) stay the same, independent of the isometric embedding. This means that the distance from a finger to a toe of a person measured along the body is always the same, independent of posture. By only considering geodesic distances or other isometric properties as done in spectral shape analysis, it is possible to retrieve all cats in a database of animals independent of the pose.

[edit] Colloquial shape definition

Further information: Glossary of shapes with metaphorical names

Shape can also be more loosely defined as "the appearance of something, especially its outline". This definition is consistent with the above, in that the shape of a set does not depend on its position, size or orientation. However, it does not always imply an exact mathematical transformation. For example it is common to talk of star-shaped objects even though the number of points of the star is not defined.

[edit] Philosophical skepticism of definitions

In Plato's Meno, Socrates questions Meno as to the most accurate definition of a figure/shape. By showing the possibility of there being more than one definition, Socrates shows that a definition cannot wholly and accurately describe something and that there is no one absolute definition for anything including shape.^[3]

[edit] Shape analysis

Main article: Statistical shape analysis

The modern definition of shape^{[clarification needed]} has arisen in the field of statistical shape analysis. In particular Procrustes analysis, which is a technique for analyzing the statistical distributions of shapes. These techniques have been used to examine the alignments of random points. Other methods are designed to work with non-rigid (bendable) objects, e.g. for posture independent shape retrieval (see for example Spectral shape analysis).

[edit] Similarity classes

All similar triangles have the same shape. These shapes can be classified using complex numbers in a method advanced by J.A. Lester^[4] and Rafael Artzy. For example, an equilateral triangle can be expressed by complex numbers 0, 1, (1 + i √3)/2. Lester and Artzy call the ratio

S(u,v,w) = (u −w)/(u − v) the shape of triangle (u, v, w). Then the shape of the equilateral triangle is

(0–(1+ √3)/2)/(0–1) = ( 1 + i √3)/2 = cos(60°) + i sin(60°) = exp(i π/3).

For any affine transformation of the Gaussian plane, z mapping to a z + b, a ≠ 0, a triangle is transformed but does not change its shape. Hence shape is an invariant of affine geometry. The shape p = S(u,v,w) depends on the order of the arguments of function S, but permutations lead to related values. For instance,

Also

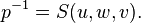
Combining these permutations gives Furthermore,

These relations are "conversion rules" for shape of a triangle.

The shape of a quadrilateral is associated with two complex numbers p,q. If the quadrilateral has vertices u,v,w,x, then p = S(u,v,w) and q = S(v,w,x). Artzy proves these propositions about quadrilateral shapes:

1. If then the quadrilateral is a parallelogram.
2. If a parallelogram has |arg p| = |arg q|, then it is a rhombus.
3. When p = 1 + i and q = (1 + i)/2, then the quadrilateral is square.
4. If and sgn r = sgn(Im p), then the quadrilateral is a trapezoid.

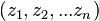A polygon has a shape defined by n – 2 complex numbers 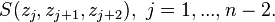The polygon bounds a convex set when all these shape components have imaginary components of the same sign.^[5]There are dirfehfhdfkjsfhksjfhsdwjkfhmxdnc207.219.69.249 (talk) 00:50, 26 October 2012 (UTC)

[edit] References

1. ^ Kendall, D.G.. "Shape Manifolds, Procrustean Metrics, and Complex Projective Spaces". Bulletin of the London Mathematical Society 16 (2): 81–121. doi:10.1112/blms/16.2.81.
2. ^ Here, scale means only uniform scaling, as non-uniform scaling would change the shape of the object (e.g., it would turn a square into a rectangle).
3. ^ Plato, Benjamin Jowett (1946). Meno. Forgotten Books. ISBN 1-60620-007-0, 9781606200070. http://books.google.com/?id=p3oQoPm-b_cC&dq=plato+meno.
4. ^ J.A. Lester (1996) "Triangles I: Shapes", Aequationes Mathematicae 52:30–54
5. ^ Rafael Artzy (1994) "Shapes of Polygons", Journal of Geometry 50(1–2):11–15

[edit] External links

Look up shape in Wiktionary, the free dictionary.

• Answers for many questions related to shapes and sizes of common objects
• American artist Allan McCollum's project to create a unique "shape" for every individual on the planet
• Shape Stencils from Stencil Ease