Magic Circles

From Wikipedia, the free encyclopedia
Blogger Ref Link http://www.p2pfoundation.net/Multi-Dimensional_Science

Jump to: navigation, search

Yang Hui's Magic concentric Circles

Magic circles were invented by the Song Dynasty (960–1279) Chinese mathematician Yang Hui (c. 1238–1298). It is the arrangement of natural numbers on circles where the sum of the numbers on each circle and the sum of numbers on diameter are identical. One of his magic circles was constructed from 33 natural numbers from 1 to 33 arranged on four concentric circles, with 9 at the center.

Contents

 [hide] 

• 1 Yang Hui magic circles
  • 1.1 Yang Hui magic concentric circle
  • 1.2 Yang Hui magic eight circles in a square
  • 1.3 Yang Hui Magic Nine circles in a square
• 2 Ding Yidong magic circles
• 3 Cheng Dawei magic circles
• 4 References

Yang Hui magic circles[edit]

Yang Hui's magic circle series was published in his Xugu Zhaiqi Suanfa《續古摘奇算法》 (Sequel to Excerpts of Mathematical Wonders) of 1275. His magic circle series includes: magic 5 circles in square, 6 circles in ring, magic eight circle in square magic concentric circles, magic 9 circles in square.

Yang Hui magic concentric circle[edit]

Yang Hui's magic concentric circle has the following properties

• The sum of the numbers on four diameters = 147，
  • 28 + 5 + 11 + 25 + 9 + 7 + 19 + 31 + 12 = 147
• The sum of 8 numbers plus 9 at the center =147;
  • 28 + 27 + 20 + 33 + 12 + 4 + 6 + 8 + 9 = 147
• The sum of eight radius without 9 =magic number 69: such as 27 + 15 + 3 + 24 = 69
• The sum of all numbers on each circle (not including 9) = 2 × 69
• There exist 8 semicircles, where the sum of numbers = magic number 69; there are 16 line segments(semi circles and radii) with magic number 69, more than a 6 order magic square with only 12 magic numbers.

Yang Hui magic eight circles in a square[edit]

Yang Hui 8 magic circles in a square 八阵图

64 numbers arrange in circles of eight numbers, total sum 2080, horizontal / vertical sum =260.

From NW corner clockwise direction, the sum of 8-number circles are:

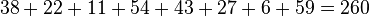
Also the sum of the eight numbers along the WE/NS axis


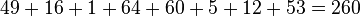
Furthermore, the sum of the 16 numbers along the two diagonals equals to 2 times 260:

Yang Hui Magic Nine circles in a square[edit]

Yang Hui 9 magic circles in a square 连环图

72 number from 1 to 72, arranged in nine circles of eight number circle in a square; with neighbouring numbers also forming four additional 8-number circles:
form out of the borders of the following 8-circles:

(NW,N,W,C)

(NE,N,E,C)

(SW,S,W,C)

(SE,S,E,C)

thus making a total of 13 8-circles in a square：

NW,N,NE,E,SE,S,SW,W,C(center),(NW,N,W,C),(NE,N,E,C),(SW,S,W,C),(SE,S,E,C)

• Total sum of 72 numbers 2628,
• sum of eight numbers in any 8-number cicles (13 in all)=262
• sums of three circles along horizontal lines= 876
• sum of three circles along vertical = 876;
• sum of three 8-circles along the diagonals =876.

Ding Yidong magic circles[edit]

Ding Yidong magic circles

Ding Yidong was a mathematician contemporary with Yang Hui, in his 6th order magic circle with 6 rings, the 5 out rings have connection with a 3rd order magic square: the unit number of the 8 numbers on any ring form a 3rd order magic square.

4	9	2
3	5	7
8	1	6

Method of construction:

Let radial group 1 =1,11,21,31,41

Let radial group 2=2,12,22,32,42

Let radial group 3=3,13,23,33,43

Let radial group 4=4,14,24,34,44

Let radial group 6=6,16,26,36,46

Let radial group 7=7,17,27,37,47

Let radial group 8=8,18,28,38,48

Let radial group 9=9,19,29,39,49

Let center group =5,15,25,35,45

Arrange group 1,2,3,4,6,7,9 radially such that

• each number occupies one position on circle
• alternate the direction such that one radial has smallest number at the outside, the adjacent radial has largest number outside.
• Each group occupies the radial position corresponding to the number on the Luoshu magic square, i.e., group 1 at 1 position, group 2 at

2 position etc.

• Finally arrange center group at the center circle, such that

number 5 on group 1 radial

number 10 on group 2 radial

number 15 on group 3 radial

...

number 45 on group 9 radial

Cheng Dawei magic circles[edit]

Cheng Dawei, a mathematician in the Ming dynasty, in his book Suanfa Tongzong listed several magic circles

• 
• 
• 

References[edit]

• Lam Lay Yong: A Critical Study of Hang Hui Suan Fa 《杨辉算法》 Singapore University Press 1977
• Wu Wenjun (editor in chief), Grand Series of History of Chinese Mathematics, Vol 6, Part 6 Yang Hui, section 2 Magic circle (吴文俊 主编 沈康身执笔 《中国数学史大系》 第六卷 第六篇 《杨辉》 第二节 《幻圆》) ISBN 7-303-04926-6/O

Retrieved from "http://en.wikipedia.org/w/index.php?title=Magic_circle_(mathematics)&oldid=545083086"

Categories:

• Chinese mathematics
• Song Dynasty